Knowing how to assess a heat sink's performance effectively is necessary today, making thermal resistance conductivity, thermal resistance values, and thermal resistance calculation essential consideration components in a thermal engineer´s workflow.

Due to the trend to downsize electronics and improve electrical resistance and general design thermal resistances, heat flux densities continue to rise.
This is a direct implication of Moore's law for microelectronics. Moore's law observes that the number of transistors in a microchip doubles approximately every two years, while the cost per transistor decreases. This trend has enabled the rapid development of increasingly powerful and affordable computing technology.
Due to this trend, heat sink performance (and calculating thermal resistance) is arguably more important than ever. Before explaining how to calculate heat sink thermal resistance, we will cover some key terminology.
What are thermal resistance and electrical resistance?
Thermal resistance is a measurement of the ability of a material to resist the heat flow through it. Thermal resistances are the temperature difference across a material divided by the rate at which heat flows through the material. The unit of thermal resistance is degrees Celsius per watt (°C/W).
Electrical resistance and thermal resistance are different variables, but they are related in that materials that are good at conducting electricity are typically also good at conducting heat. Conversely, materials that are poor conductors of electricity are also poor conductors of heat, which leads to high thermal resistance.
A material's total thermal resistance and predisposition to transferring heat depend on several factors, including its thermal conductivity, thickness, and surface area.
Thermal resistance testing uses a heat flow meter to measure the heat transfer rate through a material. The heat flow meter consists of two temperature sensors separated by a known distance, and a heat source. The thermal resistance can be calculated using Fourier's Law of Heat Conduction by measuring the temperature difference across the material and the heat flux.
Thermal resistance is an essential concept in the design of thermal management systems. By understanding the thermal resistance of materials, engineers can design more efficient cooling systems for electronic devices, buildings, and other applications where heat management is critical.
What is thermal conductivity?
Thermal conductivity is a physical property that measures a material's ability to conduct heat. It is defined as the amount of heat that flows through a material per unit of time and per unit area under a temperature gradient.
Thermal resistance depends on three factors; the material's thermal conductivity, the material, the thickness of the material parallel to heat flow, and the cross-sectional area perpendicular to heat flow.
Materials with high thermal conductivity and heat transfer abilities, such as metals, have low total thermal resistance, while materials with low thermal conductivity, such as insulators, have high thermal resistance.
How does the temperature gradient measure affect thermal resistance and thermal conductivity?
The gradient measures the change in temperature over a distance in a material. In thermal conductivity, a more significant gradient indicates a greater heat transfer rate and, therefore, a higher thermal conductivity.
Temperature gradient and thermal conductivity are related in that the gradient is directly proportional to the heat transfer rate, which in turn is proportional to the material's thermal conductivity. The higher the thermal conductivity, the faster heat can be transferred through the material for a given temperature difference.
What is a heat sink?
Typically, the term ‘heat sink' defines a device used for cooling a target and reducing heat flow and heat transfer (e.g., electronics, batteries, e-motors, etc.) by an airflow.
What is a compound of a heat sink?
Heat sink compound--also known as thermal grease, thermal compound, CPU grease, heat paste, heat sink paste, and thermal interface material--is a stick paste that is used as an interface between CPU heat sinks and heat sources. This fills gaps between the CPU or other heat-generating components and the mechanical heat sink.
The term ‘cold plate' is more commonly used when the cooling medium is liquid (e.g., water, oil, glycol) instead of air.
This article broadly uses the term heat sink, encompassing the cooling of any solid with any fluid.
The thermal efficiency gain between two different heat sinks can be measured by calculating their thermal conductivity and thermal resistance. The heat sinks must be designed to cool the same heat source.
Contrary to heat exchangers – it is impossible to calculate the efficiency of a heat sink and its respective thermal resistance and thermal conductivity without comparing it to another design.
This article will compare a Diabatix generative heat sink's thermal resistance to a conventional s-shaped heat sink.

What is a heat exchanger?
When another fluid cools one fluid, this is called a heat exchanger.
Heat exchangers have different thermal conductivity parameters and goals (e.g., heat recuperation of ventilation flows) and different performance metrics. They are, therefore, not covered in this article.
The engineering trade-off in active cooling thermal management
Before we can measure thermal conductivity performance, it's important to understand the engineering trade-off.
In active cooling, a pump for liquids or a fan for air drives the flow. Active cooling has high cooling potential but introduces a clear engineering trade-off.
The higher the pump or fan flow, the higher the cooling potential, but the higher the component's cost and power requirements.
This remains true until a certain point, as the performance gain will eventually plateau due to the physics of convective heat transfer. This can be seen in Figures 1 and 2 below. Note that the lower the thermal resistance, the lower the temperature.
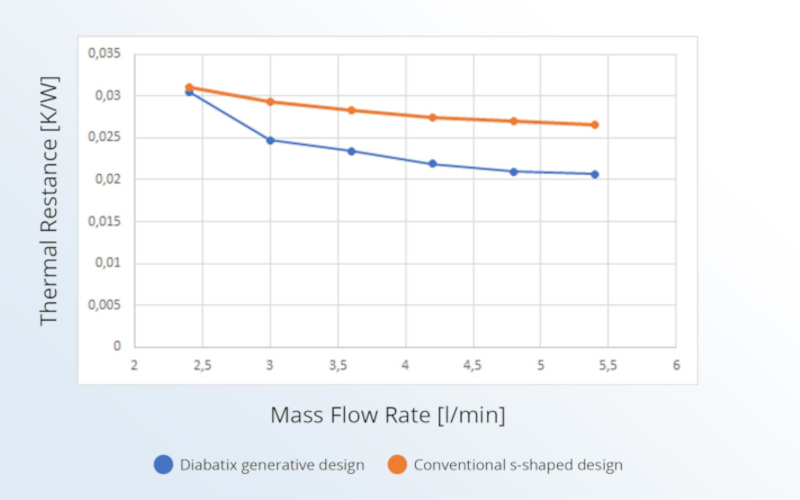
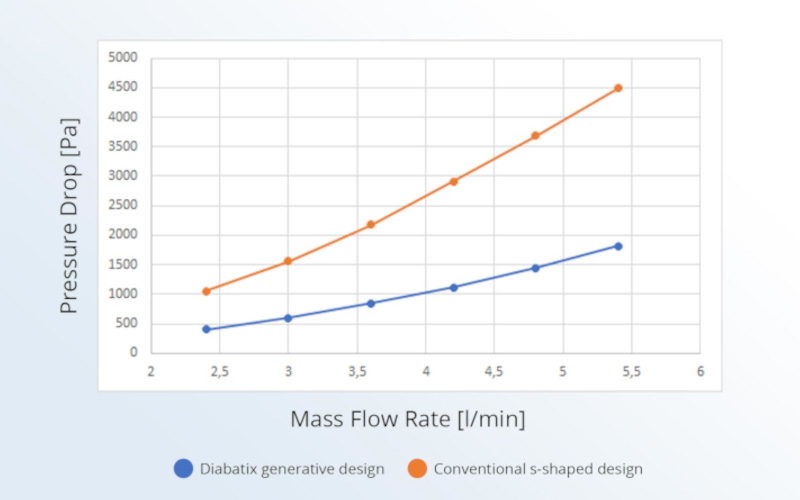
In passive cooling, the flow is driven by buoyancy, so the engineering trade-off doesn't exist, as there is no active component. This means that reliability is far better in passive cooling. However, this also implies that the design and thermal conductivity of the heat sink is all the more crucial.
Bringing a design into virtual space to evaluate thermal resistance
To evaluate the performance of a heat sink, we must first bring the design into virtual space.
That means that the design must be drawn up in a Computer-Aided Design (CAD) program and simulated with Computational Fluid Dynamics (CFD).
How to use Diabatix as a thermal resistance calculator
We use AutoDesk Inventor for the CAD and OpenFOAM for the CFD. Most of the work is done within OpenFOAM; the geometry is meshed here, with the Navier-Stokes and energy equations solved numerically.
In doing so, we arrive at a prediction of fluid velocities and temperatures throughout the heat sink that the thermal resistance depends on.
Since we specialize in heat transfer and heat flow, we have tailored our software for heat sink simulation to assess thermal resistance and thermal conductivity. This allows us to commence a simulation in just a few clicks. From there, cases are automatically meshed, refined where necessary, and effectively simulated.
At the end of a thermal resistance simulation, we check heat flow performance characteristics and the quality of the simulations.
Therefore, residuals on all governing equations must be smaller than 1e-6, and the balances on all equations smaller than 1e-4.
On top of that, we execute a mesh refinement study. This is relevant in heat transfer and flow, as an under-refined mesh generally predicts inaccurate temperatures.
Proper mesh refinement is necessary to capture thermal boundary layers accurately.
Furthermore, apart from the geometry of the heat sink itself, we obtain the specifications of the heat source (a power Q), the inlet temperature of the fluid, and the specified flow rate.
Assessing thermal conductivity performance - higher thermal resistance formulas
Now that our design geometry and specifications are known, we're ready to asses a heat sink's performance. We do that by calculating its thermal resistance.
There are four ways to define absolute thermal resistance. All involve a temperature difference divided by the quantification of the heat source.
Possible temperature differences are:
Both are called thermal resistance, although the last formula is also called thermal insulance.
Both can be used for thermal resistance with the average and maximum temperature differences specified above.
Our preferred thermal resistance formula is the first, which takes the difference between the maximal temperatures:
We prefer the highest temperature because it determines the limits of mounted components and the heating power, bringing us closer to the electrical analog for absolute thermal resistance.
Heat sink comparison - calculating absolute thermal resistance
Using the following specifications, we can use our preferred formula to calculate the thermal resistance of both the s-shaped heat sink and our generative heat sink.
Thermal resistance results
Want to calculate thermal resistance & understand thermal conductivity in a flash? Use our heat sink thermal resistance calculator tool
Below, in Figure 3, you can visualize the thermal efficiency gain percentage at various mass flow rates.
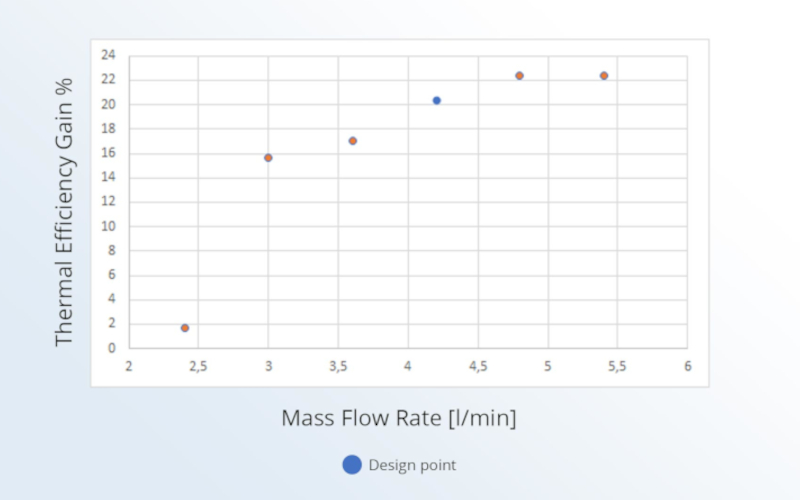
Conclusion: How to evaluate thermal resistance and thermal conductivity with Diabatix
The rise in heat flux densities due to the trend to downsize electronics calls for heat sinks that perform better than ever.
This also means that knowing how to effectively assess a heat sink's performance is necessary today, making thermal resistance calculation an essential tool in your toolkit.
Want to increase your heat sink performance without increasing or decreasing heat flow, temperature difference, temperature drop, the power dissipated, and general power requirements? Get in touch with us.
Heat Sink FAQs
What is the difference between active and passive heat sinks?
Active sinks and passive sinks are both used to dissipate heat from electronic components such as CPUs or GPUs. The main difference is that active sinks use a fan or pump to force air or liquid, while passive sinks rely on natural convection to transfer heat away from the component.
Active sinks typically provide better cooling performance than passive sinks, as the forced air or liquid can quickly remove heat. However, active sinks require additional power and can be noisy, while passive sinks are quiet and have no moving parts but may not be sufficient for high-performance applications (due to still air). The choice between active and passive heat sinks depends on the specific cooling requirements of the electronic component and the system it is used in.
Discover Related Articles
- 3 Basic Design Choices for Your Cooling System
- 3 Design Methods to Future-proof Your Heat Sink
- 4 Optimization Targets for Cooling System Design
- Calculate Heat Sink Thermal Resistance Formula
- Generative Design Is Key to Heat Sink Innovation
- Generative Design of a Liquid Cooled Heat Sink
- Generative Design: The Ultimate Solution to EV Cooling Systems
- Optimal Raspberry Pi Heat Sink in 5 Min
- Pin Fin Heat Sink Applications: Enhancing Thermal Management for Optimal Performance
- Rethinking LED Heat Sink Design with Generative Design



.jpg)
