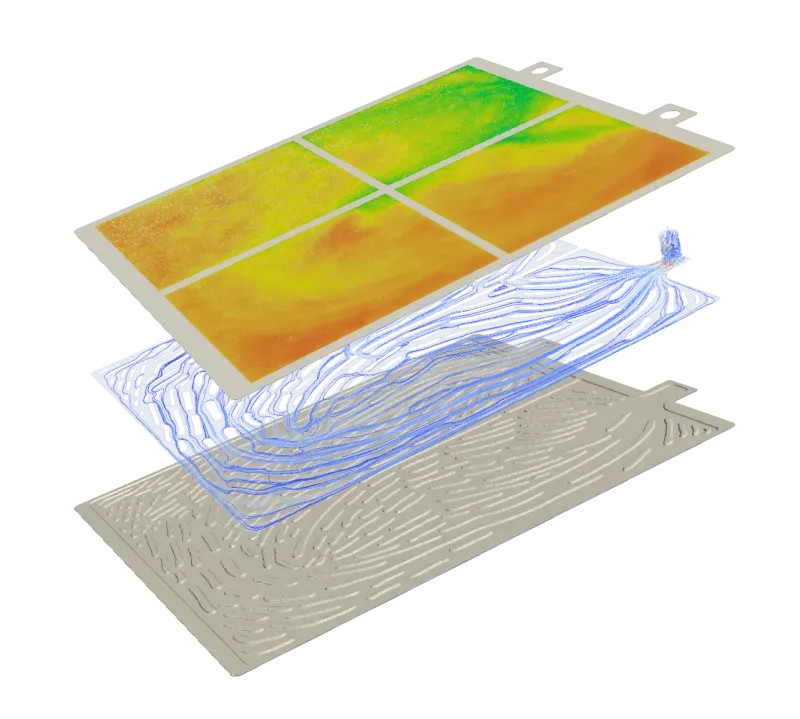
Heat sinks are cooling components that are used to facilitate heat transfer in machinery, such as motors computers and consumer electronics. With heightened concern for energy conservation and consumer demand for more powerful products, manufacturers must find innovative ways to design heat sinks that have better performance and lower production costs.
Virtual product development has been an important factor in this process of innovation. The primary aim of virtual product development is to find the optimum design of a heat sink, based on varied and sometimes contradictory requirements, the challenge is to produce geometric modifications that fit within the available space and manufacturing constraints.
Designers can use simulation software with an automated process to obtain solutions efficiently and economically, as well as to improve on current designs. These kind of software tools use advanced optimization techniques that include parametric, shape, and topology optimization. This article will discuss the advantages and disadvantages of these three optimization methods.
Parametric Optimization
Most major technological developments are improvements on existing designs. Such new designs are more or less a product of recreating components to:
• Make them fit into more limited spaces,
• Reduce their weight,
• Increase their lifespan,
• Make them easier to manufacture
In these instances, designers already have a somewhat rough idea of what the new component should look like.
As such, all they need is a novel approach to improve on the existing designs. Engineers define specific design characteristics, such as geometric data, material, and surface area of a heat sink in terms of parameters.
As an example, consider a pin finned heat sink.
Parameters defining the design can include the number of pins, the material of the heat sink, or the size of the pins.
These parameters are then varied to determine, for example, the optimal number of pins in relation to another quantity, such as the cooling air pumping power. This process is called parametric optimization.

Parametric optimization can also be used when there are no existing parts, or when a new design has changed radically such that the available components cannot be fine-tuned to fulfill the same purpose. Engineers would then create a few conceptual designs and define these designs in terms of the relevant parameters. They can then apply standard optimization methods such as Design of Experiments (DOE).
The use of parametric optimization, however, limits the number of possible solutions. It is more practical to use this method of optimization when you have knowledge or a preference of what the basic design layout should be.
Shape Optimization
Designers use the parametric optimization process to determine the optimum parameter values to achieve design objectives while meeting the set constraints. In the same way, shape optimization determines the optimal component shape for a specified objective and imposed constraints.
As an example consider the same pin finned heat sink as mentioned previously.
In shape optimization, the design variables are directly related to the mathematical functions describing the shape of the design.
The shape of the pin fins can for instance be described by a function representing the boundaries of the fins.
When the design variables, objective, and constraints are defined, the shape optimization problem can be solved by an optimization solver.
By using shape optimization however, the design freedom is limited by the fixed number of connected boundaries belonging to the design domain. The number of pin fins will thus not change when adopting this design approach.

Topology Optimization
Sometimes the quest for innovative solutions presents new challenges that designers cannot solve using iterations of old technology.
In such circumstances, new solutions have to be developed from the ground up.
When designers don't have a previous design available to base their solutions on, they can start with a plain solid and use simulation software to define a set of optimization goals and constraints. The software can then generate the optimal material configuration based on these factors.
Topology optimization is fundamentally different from other techniques since it is applied at the beginning of the design process.
The optimal geometric layout is automatically determined within a predefined design domain, whereas for parametric and shape optimization the intuition and experience of the designer play the central role in determining the initial geometric layout of the design.
The benefit of this revision to the process is that the design cycle is significantly reduced since the iterative process of providing feedback for design changes is removed.
Consider again the pin finned heat sink. When using topology optimization, all the pin fins are removed and the entire region is part of the design domain. The optimal layout can consist of organically shaped fins and may completely differ from the original pin finned layout.

Topology optimization thus starts from an empty design domain in which material is iteratively added and subtracted until an optimization target, such as maximum heat transfer, is reached. These iterations also take into account the imposed constraints, such as a pressure drop constraint.
The method generates optimal geometries for advanced thermal components heat transfer that make appliances more efficient through:
• Size reduction
• Lower operating costs
• Reduced thermal resistance
• Reduced pumping power
The topology optimization method is proving to be a very effective design method for both forced convective heat transfer and natural convection thermodynamics system components.
In recent years, the available manufacturing methods limited the ability to manufacture extremely complex shapes. The recent development of newer methods of implementing manufacturing methods such as die casting, CNC milling and extrusion, now allow for the consideration of highly sophisticated designs that were previously not possible.
These methods make it possible, for example, to construct tiny heat sinks that allow fluids to pass with minimal drag.
These highly complex models can, however, be challenging to mass-produce. Therefore, it may be necessary to put restrictions on how complex topology optimization models may become so that they are easier to manufacture.
These restrictions may include planes of symmetry, part size limitations, and unidirectional extrusion.
These restrictions help ensure that the topology optimization models are relatively easy and economical to manufacture, making the topology optimization method a realistic and promising way forward in solving current challenges in thermal design.
Discover Related Articles
- 3 Basic Design Choices for Your Cooling System
- 4 Optimization Targets for Cooling System Design
- Calculate Heat Sink Thermal Resistance Formula
- Generative Design Is Key to Heat Sink Innovation
- Generative Design of a Liquid Cooled Heat Sink
- Generative Design: The Ultimate Solution to EV Cooling Systems
- Optimal Raspberry Pi Heat Sink in 5 Min
- Pin Fin Heat Sink Applications: Enhancing Thermal Management for Optimal Performance
- Rethinking LED Heat Sink Design with Generative Design