If you are curious how Coldstream gets to the result, watch the video below, where the intermediate designs are also shown:

‍

With the end of the year holidays approaching, how about generating a Christmas tree using generative design?

How have we created the setup’s geometry?

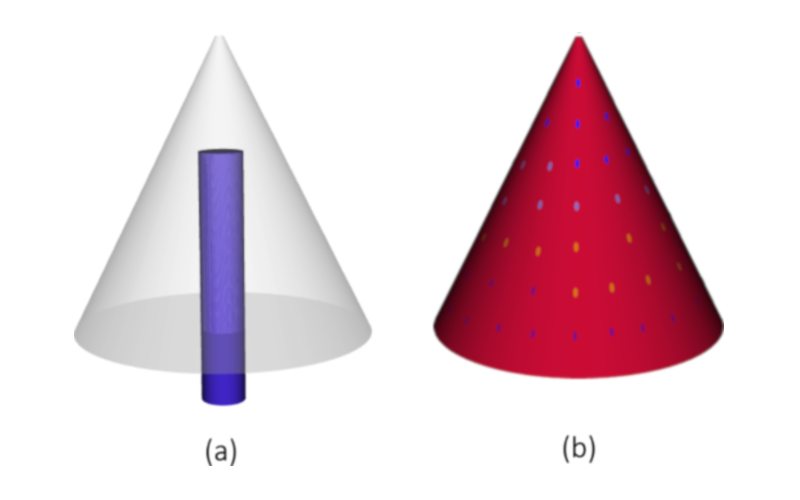
Two regions are considered for the Christmas tree: the trunk (Fig. 1a) and the body (Fig . 1b). The trunk is modeled as a cylinder made of a highly conductive material and a fixed temperature boundary condition at the bottom with a value equal to 300 K (room temperature).

The body of the Christmas tree is modeled as a cone. The lights (Fig. 1b) serve as heat sources, defined as heated wall boundary conditions with a value of 10W per light. A volumetric heat source of 500W is added. Lastly, the cone is chosen as the design region such that Coldstream computes an optimal design for the optimization problem.

Let’s explore the optimization problem!

The main issue with a Christmas tree is that the lights may become too hot and eventually stop working. For this reason, using the tree branches to reduce the lights' temperature is desirable to prevent malfunction.

Therefore, a temperature minimization objective and a maximum relative volume constraint on the design region are applied to the lights. The maximum relative volume constraint limits the area's material; otherwise, the trivial solution, the entire cone with the highly conductive material, might be returned. Mathematically, the objective function is formulated as follows:

Moreover, the constraint can be formulated in the following manner:

Are you ready to check the final result?

The final design generated is shown in Fig. 2.

‍

With this lovely Christmas tree generated by ColdStream, we would like to wish you all the best as you embark on the new year ahead!

If you want to know more about ColdStream, visit our topology optimization page and don’t hesitate to contact us.