Are you curious to go over all the iterations of the optimization process? Watch the design evolution video for this manifold:
In engineering, many appliances have components that must operate in parallel. As a result, gases or fluids must be injected at the same time in several instances. Introducing a manifold in those devices can boost the system's performance.
A manifold is an element in a machine used to distribute over or combine different flow passages of a gas or liquid. The uniformity of the flow distribution through each branch and the energy dissipation in the system defines the manifold efficiency. This means that a manifold problem is a multi-objective problem: the distribution of the incoming flow should be as uniform as possible, and a maximal reduction in energy dissipation should occur. In some cases, these objectives are complementary, while in other cases, they can counteract each other.
The Power Dissipation Minimization objective tries to minimize the energy that is being dissipated inside the fluid body. The viscous dissipation scales with the velocity gradient, so inherently, this power dissipation minimization objective will try to make the velocity field as uniform as possible, thus promoting a uniform flow distribution over the different outlets. However, geometric constraints may counteract this desire for velocity uniformity. The flow velocity would need to turn sharply to reach the first outlet than the last one, a process through which the dissipation increases.
Luckily, ColdStream can perform pure flow optimization to achieve the maximal performance of manifolds and any other gas or liquid flow-based products, such as pipes. Let's optimize the following manifold.
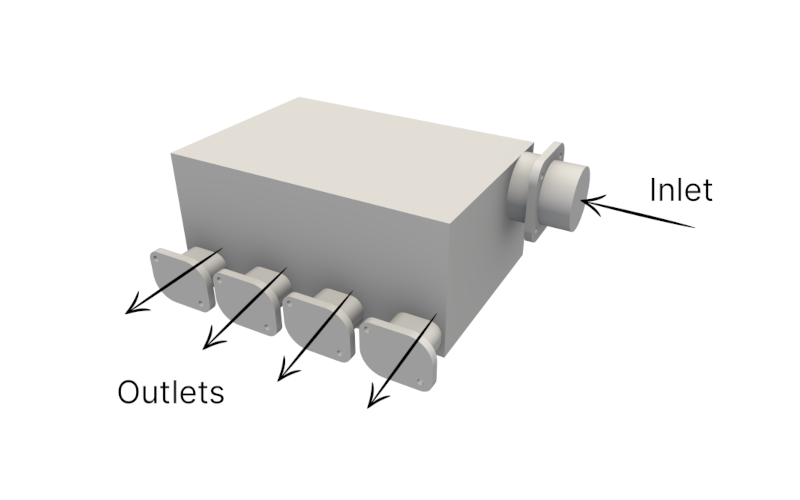
This manifold is envisioned to distribute air through 4 outlets. A fixed flow rate is established for the inlet, with an air mass flow rate of 0.048 kg/s, under an ambient temperature (20°C). The target used for the optimization is Power Dissipation Minimization, aiming to reduce the flow's viscous and pressure losses through the design. The mathematical formulation is:
Lastly, the manifold is conceived to be 3D-printing manufacturable with a 0.2mm feature thickness.
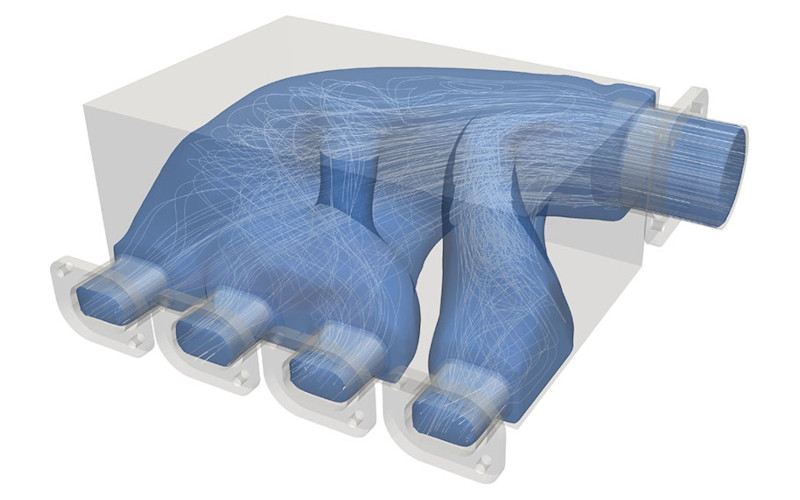
After the optimization work, ColdStream delivered an outstanding design (Fig. 2), which decreased the pressure drop to 1/3 of a conventional design.
For more information about how ColdStream can be tailored specifically to your needs, visit our topology optimization page and don't hesitate to contact our team.



.jpg)
