What Is Buoyancy & When Should I Use It?

Blog

News

What Is Buoyancy & When Should I Use It? | Diabatix

October 28, 2022

What is buoyancy?

Buoyancy is the upward-directed force exerted by a fluid that opposes the weight of a partially or fully immersed object. Buoyancy explains why some (lighter) things float in a liquid and some (heavier) objects sink. Archimedes discovered this principle over 2000 years ago!

Let’s illustrate the concept of buoyancy with a simple example. Imagine we have a cylindrical object submerged in a box of water. The water exerts a force on all sides of the cylinder, which scales with the pressure. Since the water pressure increases linearly with the depth, the force exerted at the bottom of the cylinder will be larger than the force exerted at the top of the cylinder.

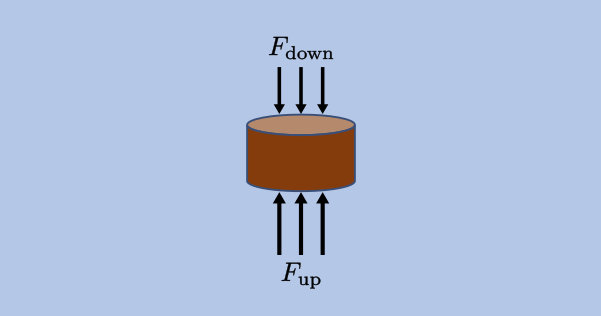
The buoyant force is the net force on the cylinder defined by:

\[F_{buoyant}=F_{up}-F_{down}=\rho_{fl}gV_{displacedfluid}\]

The buoyant force depends on the gravitational vector, the density of the fluid (in which the object is submerged), and the volume of fluid displaced by the object. The buoyant force does not depend on the mass or density of the submerged object, nor on how deep the object is submerged in the fluid.

Buoyancy imposes an upwards force which, for freestanding objects, is only counteracted by the downwards force stemming from the object’s mass. Depending on the balance between upwards and downwards forces, we distinguish between three cases:

When the weight of the object is greater than the buoyant force, the object will sink
When the weight of the object is equal to the buoyant force, the object will remain in place
When the weight of the object is lighter than the buoyant force, the object will rise upwards (if it is fully submerged) or float (if it is only partially submerged)

This is all very interesting, but what are the practical applications of buoyancy?

We propose many different cooling solutions and techniques to tackle a thermal management problem. Such cooling solutions are either active or passive cooling.

Active cooling is the employment of energy to drive a device such as a fan or pump to move fluid at a high flow rate and generate cooling using forced convection. On the other hand, passive cooling does not employ any such devices. Rather it relies on physical principles such as evaporation, radiation, and/or natural convection to do the heavy lifting.

In natural convection cases, when a heat source is warming up a fluid, the variations in fluid temperature will cause the fluid density to vary likewise, the warmer the fluid, the lower the density. Consequently, hotter fluid will rise, and cold fluid will fall and take the hot fluid’s place. This process will repeat, and in doing so, thermal energy will be convected away from the heat source. The entire concept is purely based on the physics of buoyancy and is attractive because it does not require any external energy. Buoyancy-driven natural convection (in combination with radiation) explains how most industrial passive cooling systems work.

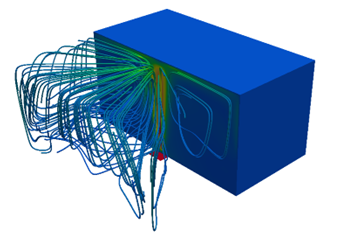
Natural convection is captured in the following image, where a small red heat source at the bottom heats the fluid causing it to rise in the middle. The fluid will in turn transfer the heat to the environment via the top surface, which cools it back down causing it to sink:

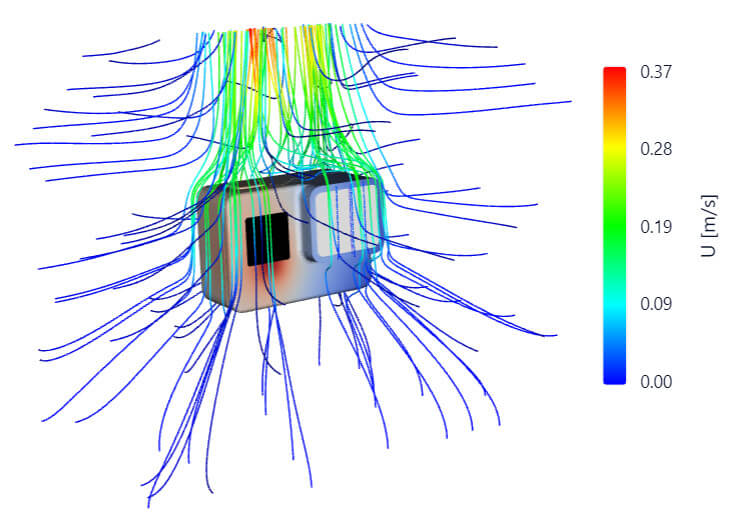
The next image below visualizes the same effect from up close. Here, an action camera produces some heat, heating the fluid next to it. This hot fluid flows upwards sucking in new fluid particles from all around it.

In forced convection cases, buoyancy is also present, but its effect is generally much smaller than the cooling effect provided by the fan or pump.

Fascinating! So, should I activate buoyancy if I want to simulate a natural convection case?

Precisely! In ColdStream, it is possible to toggle buoyancy for any case, but it is especially important to activate when the case relies on natural convection. All that is required is providing or defining a fluid material with a thermal expansion coefficient.

In ColdStream, the Boussinesq approximation is used to model the effects of buoyancy on the flow and heat transfer physics. This method assumes that the density value is constant everywhere except in the gravitational term. When performing a CFD simulation, an effective driving density \(\rho_{eff}\) is calculated based on the local temperature T as

\[\rho_{eff} = \rho(1-\beta(T-T_{ref}))\]

where \(\rho\) is the reference density, and \(T_{ref}\) the reference temperature, both of which are provided as inputs when preparing a case setup on ColdStream. Moreover, \(\beta\) is the thermal expansion coefficient, which represents how sensitive changes in density are to changes in the temperature fora given fluid. Finally, since the density variations are only important in the buoyancy term, density changes lead to buoyant effects captured in our simulations.

‍

Conclusion

Buoyancy is the upwards pointing force due to the heat up of the fluid. This effect is present everywhere in the fluid volume but can be ignored where forced convection is imposed.

For more information on how buoyancy can be used in ColdStream, visit our documentation page.

Get started with ColdStream

Discover how our generative design software will help you during every phase of the cooling design process - from optimizing first designs to virtual testing and detailed analysis.

Book a demo